" It is the glory of geometry
that from so few principles, fetched from without, it is able to accomplish
so much."
Sir Isaac Newton
[1]
Calculating Fractal Dimension
In classical geometry, shapes have integer dimensions.
A point has a dimension of
, a line has a dimension of
, an area has a dimension of
and volume has a dimension of
. From these elements--points, lines, areas and volume--we derive the basic
shapes of traditional geometry: triangles, squares, circles, cones, cubes
and spheres .
Figure 4.1 Traditional
dimensions point, line, square and cube.
We can use non-spatial
dimensions--time, color and perspective--to add dimension to otherwise
static objects. For example, you may have seen an image on a
-dimensional computer screen
that appears
-dimensional because of perspective. Using computer-generated perspective,
architects can visually walk through a entire building's design before construction
even begins see Figure 4.2 and Color Plate 22. Using color changes, scientists
can display thermodynamic heat fluctuations that can be used to indicate
venerable points with low heat dissipation. By plotting sound frequencies
over time, acoustical engineers use visual representations to show how different
harmonic patterns interact. See Figure 4.3 and Color Plate 23 to see how
changing colors can add information associated with dimension.
Figure 4.2 Computer
rendering of a
-dimensional view.
Figure 4.3 An added
dimension represented by color (shade) changes
[2]
.
By using non-spatial dimensions, mathematicians and
scientists have explored spaces beyond traditional
-dimensions. Examples include
-dimensional 'cubes' called tesseracts. These cubes when viewed in
-dimensions appear as seven
cubes that share common sides with each other see figure 4.4. While no tesseract
can physically be built, understanding these structures can offer insights
into real world problems such as optimizing a network's path to follow the
shortest distance. Physicists and
mathematicians, routinely formulate even higher dimensions, known as ordered
states, to manipulate complicated equations that would be much harder to
work with at a lower dimension. It is not uncommon for atomic physicists
to work with a dimensional space in the teens in order to keep track of
all possible states of particles found at the subatomic level.
 |
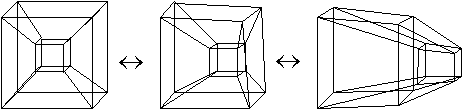Figure 4.4 Tesseract, a
-dimensional drawing of a
-dimensional object.
It is sometimes difficult to imagine these higher dimensions.
Here we have taken an excerpt from the book Flatland
[3]
a romance of many dimensions,
where Pointland, Lineland and Spaceland all see the same world differently
to aid in visualizing different dimensions.
Excerpt from Flatland
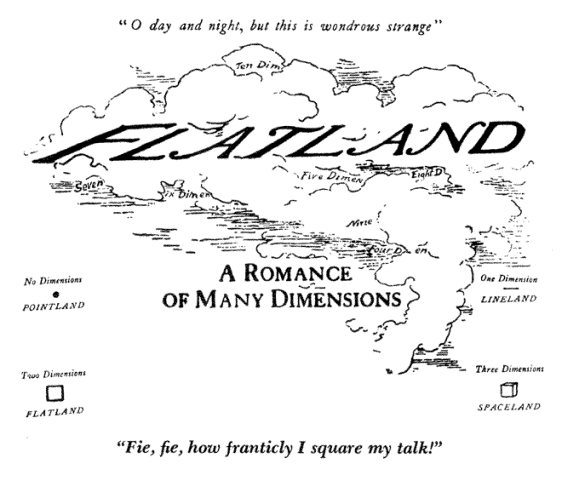
4.5 Map of lands
with different dimensions from the book Flatland.
" § 1.-Of
the Nature of Flatland
I call our world Flatland, not because we call it so,
but to make its nature clearer to you, my happy readers, who are privileged
to live in Space.
Imagine a vast sheet of paper on
which straight Lines, Triangles, Squares, Pentagons, Hexagons, and other
figures, instead of remaining fixed in their places, move freely about,
on or in the surface, but without the power of rising above or sinking below
it, very much like shadows - only hard and with luminous edges - and you
will then have a pretty correct notion of my country and countrymen. Alas, a few years ago, I should have said "my universe": but now my mind has been opened to higher views
of things.
In such a country, you will perceive at once that it
is impossible that there should be anything of what you call a "solid"
kind; but I dare say you will suppose that we could at least distinguish
by sight the Triangles, Squares, and other figures, moving about as I have
described them. On the contrary,
we could see nothing of the kind, not at least so a to distinguish one figure
from another. Nothing was visible,
nor could be visible, to us, except Straight Lines; and the necessity of
this I will speedily demonstrate.
Place a penny on the middles of one of your tables
in Space; and leaning over it, look down upon it. It will appear a circle.
But now, drawing back to the edge of the table, gradually
lower your eye (thus bringing yourself more and more into the condition
of the inhabitants of Flatland), and you will find the penny becoming more
and more oval to your view; and at last when you have placed you eye exactly
on the edge of the table (so that you are, as it were, actually a Flatlander)
the penny will then have ceased to appear oval at all, and will have become,
so far as you can see, a straight line.
The same thing would happen if you were to treat in
the same way a Triangle, or Square, or any other figure cut out of pasteboard.
As soon as you look at it with your eye on the
edge on the table, you will find that it ceases to appear to you a gure,
and that it becomes in appearance a straight line. Take for example an equilateral Triangle - who represents with us
a Tradesman of the respectable class. Fig.
1 represents the Tradesman as you would see him while you were bending over
him from above; figs. 2 and 3 represent
the Tradesman, as your would see him if your eye were close to the level,
or all but on the level of the table; and if your eye were quite on the
level of the table (and that is how we see him in Flatland) your would see
nothing but a straight line."
(1) (2) (3)
Edwin A. Abbott
•••
Now lets briefly look at mathematical
tools developed over the centuries that help us to understand fractals.
Infinite Lengths and Scale Ability a prelude to fractals.
Many of the principles found
in fractal geometry
[4]
have origins in earlier mathematics.
For example scale ability and line lengths have long been associated with
geometrical structures. In Elements, Euclid ( 330- 275 B.C. ) proposed lines
with infinite lengths to illustrate the concept of parallel lines, there
he also used self-similar triangles to show the congruency of triangles
see Figure 4.6. Archimedes (287-212 B.C.) used spirals to illustrate repeating
transformations. Later the mathematician Jacob Bernoulli (1654-1705) expanded
this idea to show that some spirals could be drawn with an infinite length,
of which the logarithmic spiral is the most famous see Figure 4.7. Another
well known spiral with infinite length is the golden mean spiral derived
from the ancient Greek's golden ratio
see Figure 4.8. This spiral closely
resembles the sea creature, nautilus seen in Figure 3.89 in Chapter 3.
Figure 4.6 Parallel lines of
infinite lengths and triangles within triangles.
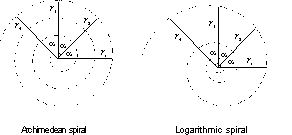
Figure 4.7 Spirals with finite
and infinite lengths.
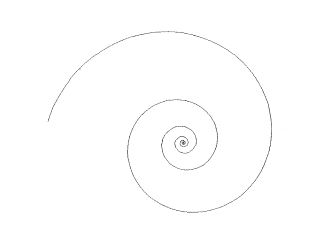
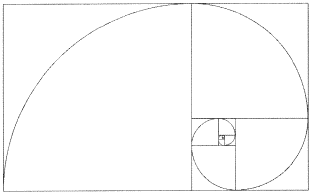
Figure 4.8 Golden ratio spiral.
Similar spirals made using
FractaSketch can be seen in Appendix B.
Along with geometrical transformations seen in scaling,
mathematical equations too can be transformed. An example of this is seen
here with logarithms and with iterated function systems in Chapter 5.
Logarithms as
Mathematical Transformation
John Napier (1550-1617) originally invented logarithms
(represented as log) to simplify multiplication. By converting two numbers
to their corresponding log values, adding them together, and then reversing
the process, he showed how a close approximate product of two numbers could
be relatively easily calculated. Before computers, logarithms were an invaluable
method for multiplying large numbers, along with solving division problems,
calculating powers and roots. Here is a list of logarithm transformations:
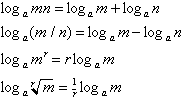
Figure 4.9 Table of Logarithm Transformations.
A logarithm's base can have any positive value. The most common values are
and
[5]
denoted by
.
Centuries later these logarithms would be crucial in
the calculation of fractal dimension as seen in the following sections.
The Hausdorff-Besicovitch Dimension
" As far as the laws of
mathematics refer to reality, they are not certain; and as far as they are
certain they do not refer to reality."
Albert Einstein
Felix Hausdorff (1868-1942)
and Abram Besicovitch(1891-1970) revolutionized mathematics by proposing
dimensions with non-integer values. They demonstrated that though a line
has a dimension of
and a square a dimension of
, many curves have an "in-between"
dimension related to the varying amounts of information they contain. We
refer to such in-between dimensions as the Hausdorff-Besicovitch dimension.
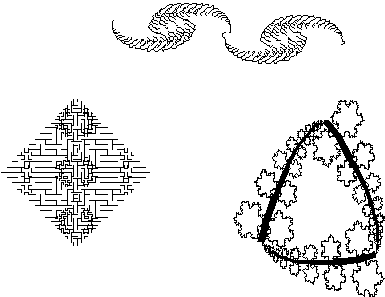
Figure 4.10 Dimensions
caught in the middle.
To explore the Hausdorff-Besicovitch dimension, we
will look first at traditional dimensions ( lines, area and volume) and
then explore expanded dimensions of fractals using three methods of calculations:
•
1. The exactly self-similar method for calculating dimensions of mathematically
generated repeating patterns.
•
2. The Richardson method for calculating
a dimensional slope.
•
3. The box-counting method for determining the ratios of a fractal's area
or volume.
Calculating
Traditional Dimensions
" One must say- instead of points, straight lines and planes
- tables chairs and beer mugs"
David Hilbert
To calculate a fractal's dimension, we simply extend
the formula for calculating traditional dimensions, so let's begin with
this basic formula. Look at the dimensional relationship of how a line,
a square and a cube are linked together dimensionally in Figure 4.11.
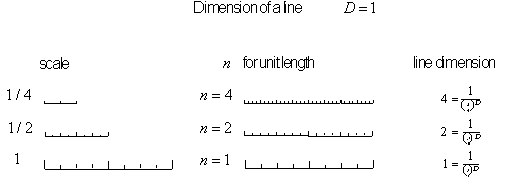
Figure 4.11. Illustration
of line segments,
and scaling factors,
raised to the appropriate dimension
.
The number of line segments
of a unit, is equal to the inverse
of the scaling factor
, raised to the appropriate dimension
.
•
The general equation is represented by:
The first three integer dimensions are
=
for a line,
=
for a square, and
=
for a cube
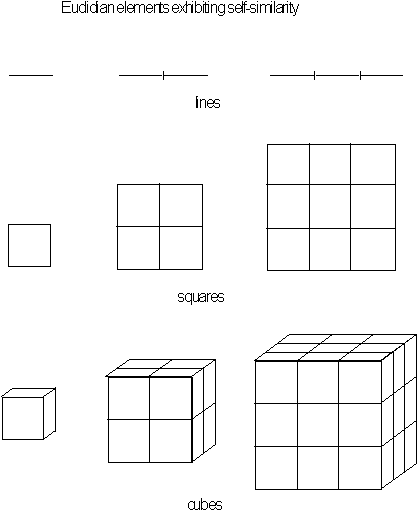
Figure 4.12 Basic
construction of lines, squares and cubes of unit lengths
,
,
.
The list below shows the number of pieces
in relationship to
vs.
, for a given line, square
and cube.
values: line
square cube
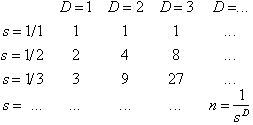
Figure 4.13. Table of the number of segments n in relationship
to
vs.
.
Though non-spatial dimensions expanded the range of
dimensions we can explore, these dimensions are still whole, or integer,
dimensions. Not until recently,
with the advent of fractal geometry, have we begun to explore partial, or
fractional, dimensions. In this section, we will look at these fractal dimensions.
Calculating Dimensions of Self-Similar
Fractals
Calculating the fractal dimension of exactly self-similar
shapes is fairly straightforward. This approach, which is limited to fractals
whose structure can be predetermined mathematically, produces precise values.
These are the linear fractals we saw in Chapter 3.
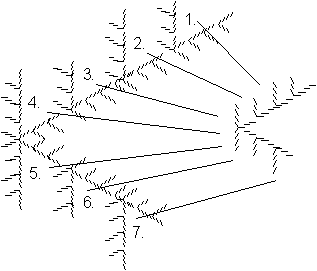
Figure 4.14 Exactly
self-similar fractal.
Recall that the basic equation for calculating dimension
is:
Although there is no rule that dimension
has to have an integer value, this has been the convention in traditional
geometry. Here we will carry out numeric calculations, for many different values of
and
, where
is not an integer dimension, but rather a 'fractional' or 'partial'
dimension.
Given:
the familiar case.
take
of both sides.
factor the exponent
out of the scale factor.
divided by
to set the equation equal to
.
We are left with the equation:
In a true mathematical fractal,
replacing the line segments with seeds is a never ending process.
Therefore the general case
is written
, where
represents the level the fractal "seed" has been replicated.
Which gives
where
= the level of replication.
However since
is found in both the nominator and the denominator of the equation
it can be neatly factored out, so we are still left with the basic equation:
where the exponent
is factored out .
The formal fractal dimension
equation for
is given as the
.
Calculating the
Dimension of the Koch Curve
Now
lets apply the formula that we have derived in the previous section to the
Koch curve. This curve makes a good example because its construction is
uniform and we can calculate its dimension with relative ease.
Figure 4.15 Koch
curve showing
levels for
and
values.
From Chapter 3, we know the number of line segments
in the Koch curve is
and that each line segment is replaced
by a replica of the original, reduced in scale by
. To calculate the dimension:
•
Use the basic dimension equation
.
•
Replace
with
, for the number of unit line segments and
with
, for the scale factor. The equation now becomes
, or simply
.
•
To find
, take the log of both sides. Simplify and you are left with
.
Now lets use what we just learned to calculate the
dimension for the Koch Snowflake.
The Dimension
calculated for the Koch Snowflake
The Koch Snowflake can be created using two distinctive
techniques. One method used assembles the Koch Snowflake from perimeter
components of the Koch curve, the other method produces the entire the Koch
Snowflake from a single generated curve.
Perimeter
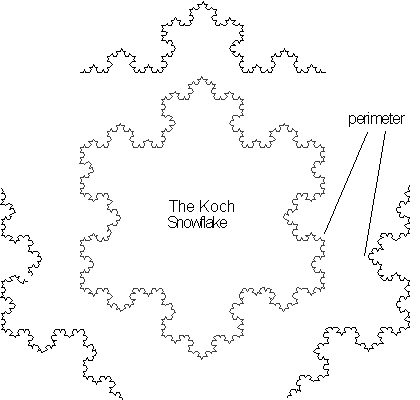
Figure 4.16 The
Koch snowflake constructed by connecting edges of the Koch curve shown with
.
The first technique uses three Koch curves which are
joined together at the edges as seen in Figure 4.16 to form the Koch snowflake.
Since the construction of these curves involves calculations only involving
the outer boundary, the fractal dimension calculated will be that of its
perimeter, the Koch curve.
Inner dimension
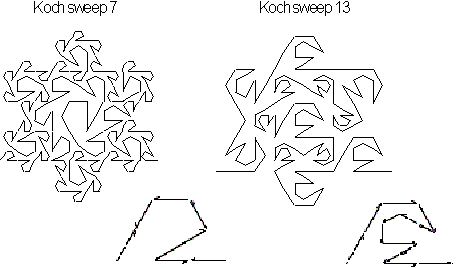
Figure 4.17 Two
different seeds producing the Koch snowflake.
The second technique involves the construction of the
whole Koch snowflake from a single seed. Many varying seeds can be used
as seen in Figure 4.17. Since the entire snowflake is formed from a single
seed the calculated dimension will be that of the entire curve.
Now lets look at the dimension of one variety call
the 7 Snowflake Sweep. As seen from the curve not all replacement components
have the same length, so the basic equation for calculating the exact dimension
can not be used here. So then how do we
calculate its dimension? We
begin by looking at how the overall snowflake curve is formed. The basic
seed has 7 line segments with 6 reduced by
scale and 1 reduced by
scale. If all the line segments
were reduced by the scale
the dimension equation would be
simply
. However, since at least one segment is reduced by a scale
of a lesser amount, namely
, the dimension of the curve has to be greater and a ratio relationship
has to be establish between the different scaling values.
The equation we use
to develop this ratio relationship is given by
.
For the Snowflake Sweep's exact calculation is given
by
. Calculating the dimension form this equation
we find
.
This value corresponds to the observed value, dimension
, of the Snowflake Sweep curve that covers the area of a plane. This region
is referred to as its inner dimension.
As we have just seen the Koch Snowflake actually has
two types of dimensions: one for its perimeter and one for its inner region.
In the following section we will see how to numerically calculate other
exactly self-similar fractals with varying
scaling values.
Other curves
with a perimeter and inner dimension.
All fractal curves with area ( inner dimension
) also have a perimeter dimension. Here we will look at two more examples:
the Gosper island and later the Dragon curve. Some fractals with an inner
dimension of less than
also have an alternate perimeter dimension, as we will see with the
Monkey Tree fractal. As shown with the Koch Snowflake, dimensions calculated
relate to the specific seed used to construct it. For example if a perimeter
curve is used to create a fractal, that curve's dimension relates to its
boundary, accordingly if a curve's construction is that of a complete fractal
the dimension calculated will be that of its entire structure.
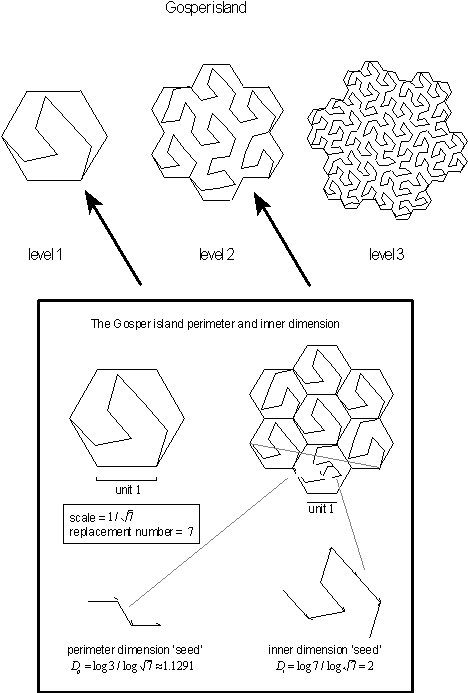
Figure 4.18 Gosper
island with both perimeter and inner dimension.
As with the Koch snowflake, the Gosper island
[6]
too can be created by placing
perimeters together or from a single seed. The calculated perimeter dimension
is given by
segment lengths each reduced by
a scale s of
. This results in a perimeter dimension that is calculated to be
. Since entire Gosper curve fills an area it has an inner regional dimension
of
. This can be seen in Figure 4.21 that shows a numerically calculated value
of
.
Figure 4.19 Calculating the Gosper island in the plane
dimension.
Now lets look at calculating an exact fractal with
different segment lengths whose inner dimension is less than
.
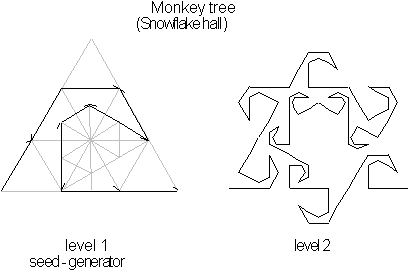
Figure 4.20 The
Monkey Tree's seed generator and its next growth level.
The Monkey Tree
[7]
seed uses two different segment
lengths for
, each with a different scaling value for
to generate its fractal, six with
=0.333 and five with =0.186. Its over all dimension is given by the segment's
ratio where
or
.
Monkey Tree Maze Game.
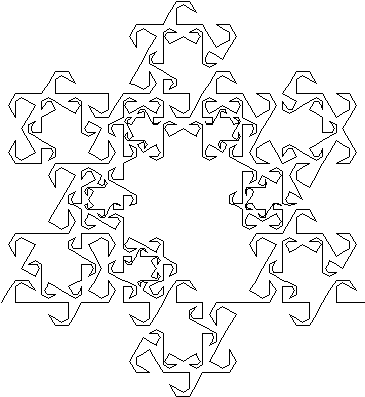
Figure 4.21 Monkey
Tree Maze.
The Monkey Tree curve makes for a visually appealing
maze with its many turns and empty regions. Since the Monkey Tree is created
from one continuous curve that never overlaps, a path can be made from any
region that escapes to the outside. To see this more clearly randomly choose
a section within the curve in Figure 4.21 and see how fast you can find
a way out. If you get stuck you can follow the curve path for the exit.
Calculating the
Dimensions of the Varying Dragon Curves
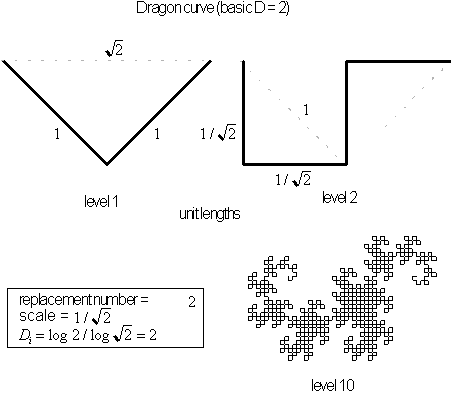
Figure 4.22 Component
lengths and completed form of the Dragon curve.
We begin our calculation of the dragon curve's dimension
with its most basic construction, in which two seed segments of length
replaces a single line segment with
length
. This results in a scale reduction,
, of
. The dimension is calculated to be
. This curve is contained and fills a region with a confined area as seen
in figure 4.22.
The dragon curve comes in variety of forms with differing
dimensions. In the following section we will see some of these variations.
Now lets look at what happens if we lower the fractal
dimension of the seed for the basic dragon curve.
Lower dimensions,
its area disappears.
If line segments were shortened the fractals dimension
would be reduced and it would no longer cover an area. This can be done
by shortening seed segments at the same time keeping the starting and ending
points constant or by increasing the distance between the beginning and
end points. For illustrations on dragon curves with dimensions less than
dimension-
see figure 4.23.
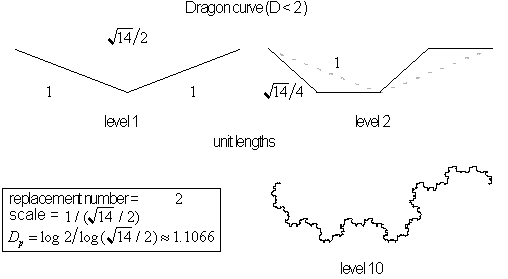
Figure 4.23 Dragon
curves with dimension less than
.
Now lets look what happens to a dragon curve whose
component lengths (generator) are increased in relationship to its overall
length (initiator).
Higher Dimension
Seeing How Some Fractals Can Grow Forever.
If we decrease the Dragon Curve seed's segment angle
its calculated dimension would also increase. This can be done by lengthening
seed segments at the same time keeping the starting and ending points constant
or by reducing the distance between the beginning and end points of the
seed. Unlike other fractals we have seen earlier, which are limited to an
confined space, fractals with 'calculated'
dimension greater than
can continue to expand outwardly
from the center forever. If a seed segment line is longer than the distance
between the starting point and the ending point of the seed the fractal
will diffidently continue to do so, see Figure 4.24.
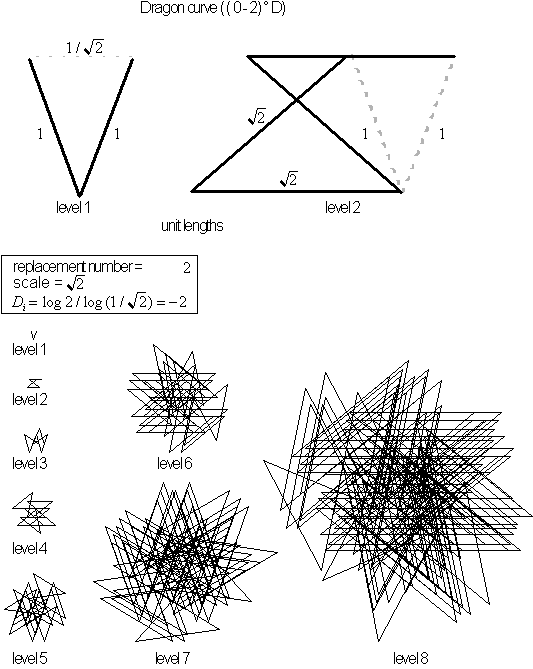
Figure 4.24 Dragon
curve with scaling value greater than
.
Now what would happen when we use two line replacements
whose lengths are greater than
. The new 'calculated' dimensions will fall in 3 parts:
I. scale
, where the dragon structure grows continuously in relation to its scaling
factor and its calculated dimension range is
.
II. scale
, a special case where all 'seed' replacements over lap causing a growing
triangular grid with uniform density, see Figure 4.25.
III. scale
where 'calculated' dimensions have negative values and the fractal will
always continue to expand for higher levels of the curve.
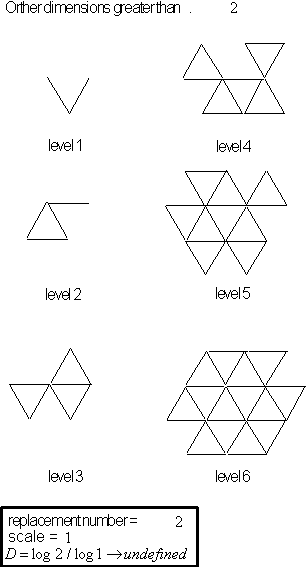
Figure 4.25 Dragon
curve with a scaling length equal to segment length.
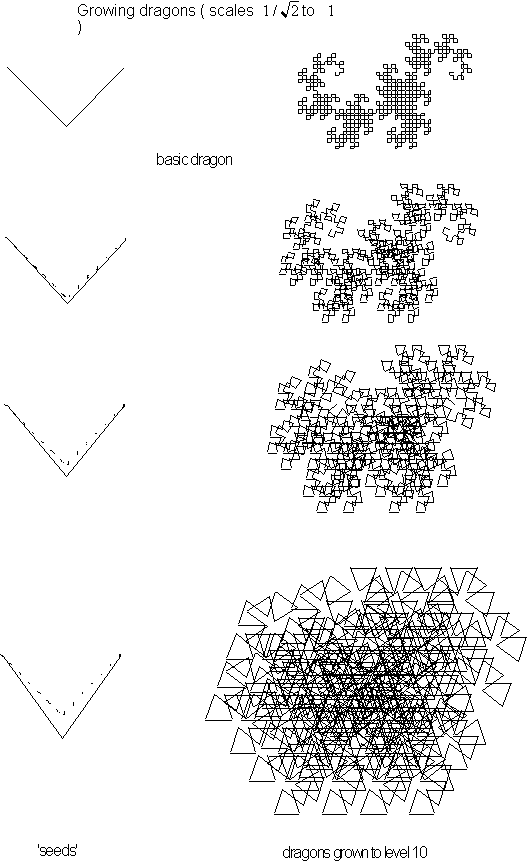
Figure 4.26 Four,
2 segment replacements with continually longer segment lengths and their
growth.
Does this mean that our new fractal is greater than
-dimensional? In the physical and mathematical world, the answer is no because
it is constrained to a
-dimensional plane. In theory, however, the answer 'could be' yes, a somewhat
philosophical answer. The dragon
curve contains more mathematical information than is needed to fill a plane.
If we could find a way to liberate this fractal from its confined space,
its high dimensional curves could fill up a volume space (similar to the
way the twisted Hilbert curve segments do in Chapter 3). In fact, some could
even conceivably fill up a
-dimensional space or greater if we could find one for it to exist in. These
principles hold true for other linear fractals too as we will shall see
using FractaSketch.
Let use FractaSketch to build an ever expanding fractal.
Using FractaSketch to Build an ever-growing
fractal.
Figure 4.27 Dragon
with line segments greater than the its seed length.
Here we will use FractaSketch to grow fractals whose
mathematical dimensions are calculated to be greater than
. A dragon seed works nicely, but any other fractal seed following the same
instructions should also work.
Step 1: Open a drawing pallet and
create a small fractal with at least one line segment that is longer than
the distance between the beginning and end points, as in Figure 4.27.
Step 2: Click on levels 2-10 to watch
the fractal grow. Notice that the
fractal continues to take up more and more area on the computer screen until
the screen in completely covered see Figure 4.28. The rate of growth depends
on the length of the seed's segment used. If the growth rate is very rapid
you can use the "Reduce" feature from the "Scale" menu
as often as needed to get a more complete view.
Step 3: Repeat the growth process
with seed lines of various lengths.
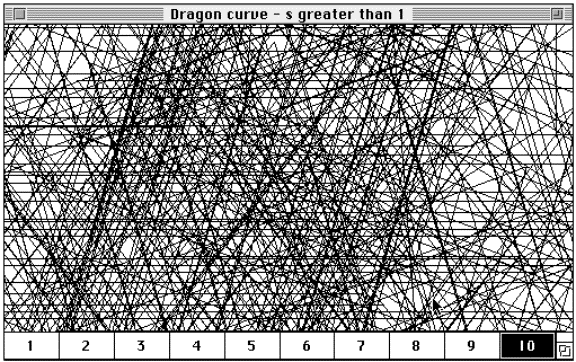
Figure 4.28 A growing
fractal 'seed' in FractaSketch that will increase in size at each higher
level.
FractaSketch gives fractals that continue to grow uncontrollable
an uncertain calculated value of "??" in its menu bar, see Figure
4.29.
Figure 4.29 Menu bar with uncertain dimension.
Now lets use what we have learned in pervious sections
to calculate the dimensions and apply these principles to objects that reside
in a volumetric space. Here we will look at two such examples: the Menger
sponge and the Sierpinski tetrahedron or
pyramid.
Calculating Dimensions
for the Menger sponge and Sierpinski Pyramid or tetrahedron
Figure 4.30 Components
of the Menger sponge.
The Menger sponge consists of a primary cube divided
equally into 27 smaller cubes, each a 1/3 scale copy of the original. Then the center cubes are removed from all
6 sides and the middle, leaving 20 smaller cubes. By using the exact method
formula we get a calculated dimension
for the Menger sponge of
. An object residing in a 3-dimensional space whose components take up no
volume.
Note, if you take a line connecting any corner diagonal
points of the Menger sponge, their intersection would be that of the Cantor
set for that length.
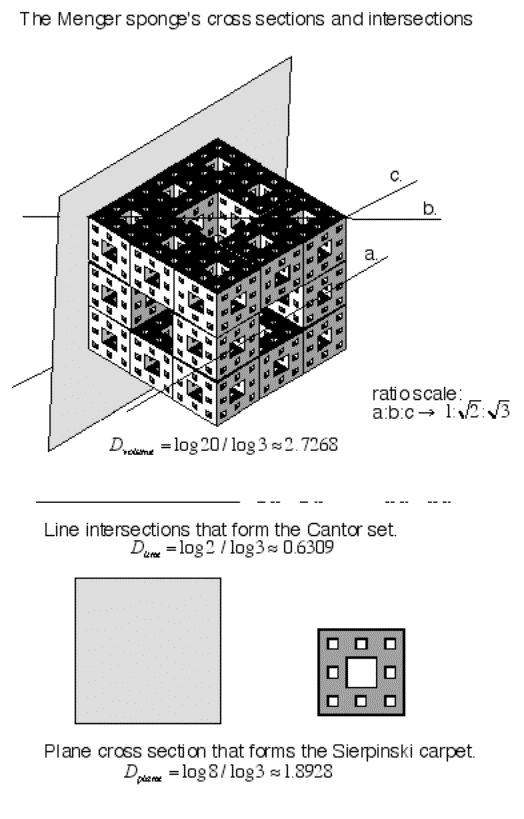
Figure 4.31 The
Cantor set found in the Menger sponge.
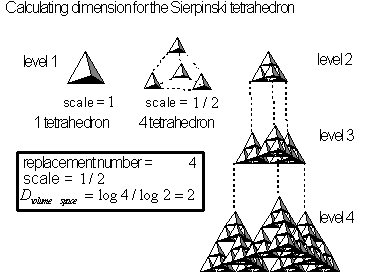
Figure 4.32 Calculating
a Sierpinski pyramid (tetrahedron) dimension.
The Sierpinski pyramid consists of a primary pyramid
that is replaced by
smaller pyramid each
the original scale. The calculated
dimension is equal to
. The Sierpinski pyramid gives an example of a
dimensional object without area.
If such a pyramid existed, it would reside in a volumetric space with its
physical structure not taking up any volume space, even though its residing
space would be defined.
How are these Fractals Alike ?
Can you guess what the fractals is Figure 4.33 have
in common ?
Figure 4.33 Assortment
of fractal images.
Answer: They all have a fractal dimension of roughly
1.5. If you look carefully you can
see that though each fractal has a different form, they all cover a similar
amount of the
-dimensional plane.
Next we will play the Totem Pole game in which we will
place fractals in order of their dimension.
The Fractal Totem Pole Game
There are a number of objects in Figure 4.35 below, and each has been generated using a
number of equal line segments. Then the segments have been replaced with
a small replica of the whole object. This was repeated 4 times (level 4).
The goal of the game is to put the objects in order of their fractal dimension,
and to find their underlining seed-shape.
Hints: 1) divide the object into halves or thirds,
2) look at the ends for a recognizable seed-shape of the whole, 3) check
the density of area being covered. Generally, the more solid the area is,
the higher the fractal dimension. Also notice disproportionately long lines,
as they generally indicate lines that have not been transformed.
Figure 4.34 Images to put in order of their fractal
dimension.
Now use FractaSketch to see if you can create totem
pole fractals, if you haven't done so already.
Answers to the Totem Pole Game showing a list of their
exactly calculated fractals can be seen on the next page.
Figure 4.35 The Totem Poles seeds and their corresponding
dimensions.
For examples of other fractals with exactly calculated
dimensions see Gallery of Fractals in Appendix B.
In the next section
we will use another method to calculate fractal dimension. This technique
called the Richardson method is generally used when an object has a fractal
structure that is not exactly repeating, such as a coastline, and therefore
the exact method can not be applied.
The Richardson's Method of
varied measured lengths.
" Big whorls have little whorls,
Which feed
on their velocity;
And little
whorls have lesser whorls
And so on
to viscosity
(in a molecular sense). "
- Lewis Fry Richardson
[8]
Lewis Fry Richardson (1881-1953), an English meteorologist, pioneered a process
for calculating dimensions with varied measurements. Using this technique
an object's perimeter is measured with rulers of different lengths, then
by graphing its slope the corresponding dimension is calculated. His work
compared the dimensional slopes of coasts, such as Great Britain, that remain
jagged at many levels of magnification, to non-fractal boundaries like circles
that remain smooth
[9]
.
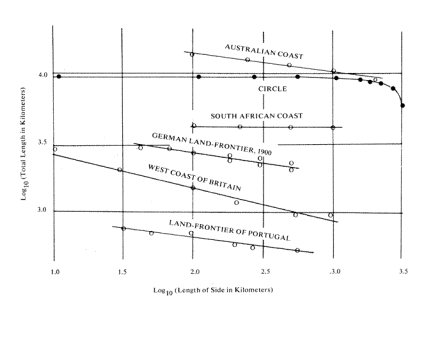
Figure 4.36 Dimensions
of coastlines vs. a circle, Richardson's calculations. Illustration from
The Fractal Geometry of Nature, © 1982 Benoit Mandelbrot.
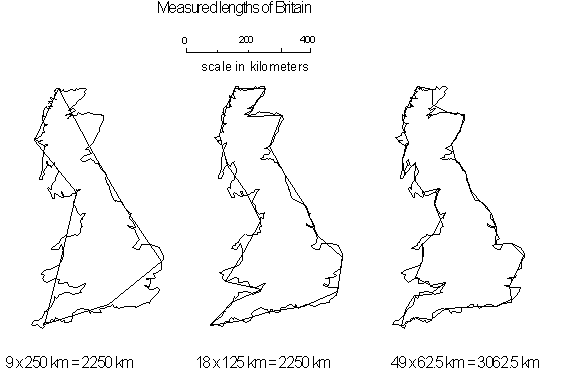
Figure 4.37 Measured
segments for the coast of Britain
[10]
.
Though Richardson
[11]
had spent many years in researching
boundaries, it was not until 1961, eight years after his death, that the
results of his experiments were published. In his paper, Richardson
points out that countries with common borders often report different
border lengths as he notice from examining various encyclopedias. For example,
Spain claimed its boarder with Portugal was 987 km, whereas Portugal claimed
it was 1214 km . Similarly, Holland claimed its border with Belgium was
380 km, whereas Belgium claimed it was 449 km.
Through graphs, Richardson tries to explain what accounts
for these relatively large differences in measurements, often varying as
much as 20%.
[12]
He suggests that the different
'measuring sticks'
[13]
used by one country might
be disproportionally shorter, maybe even by an
factor of
, than what an other country uses. Also, a small country might take more care in measuring its boarder
than a large country that has a greater perimeter to cover.
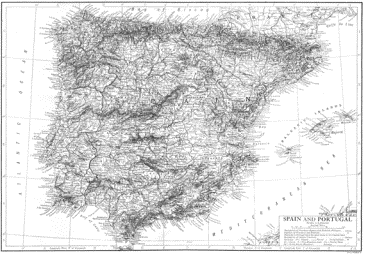
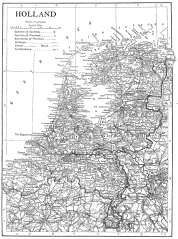
Figure 4.38 Borders of Spain and Portugal and borders
of Holland and Belgium.
This method that Richardson developed, also known as
varying slope dimension or compass dimension, is an effective technique
for measuring an object's perimeter fractal dimension. Although not as precise
as the method used for exactly self-similar objects, this procedure enables
us to calculate the dimensions of real-world objects, which are not perfectly
self-similar.
To calculate the dimension of perimeters with the Richardson
Method, you use 'rulers' of differing lengths. Then by comparing the measured
lengths of an objects perimeter to corresponding variations in ruler lengths
and plotting the results, a graph can be made with logarithmic scales, from
whose slope an object's dimension can be readily calculated. Logarithmic
scales are used because the exponent values associated with dimension, translate
easily to linear values that define
a slope. It is the object's structural changes, weather it becomes more
detailed or smoother, at various scales that is the object's fractal dimension.
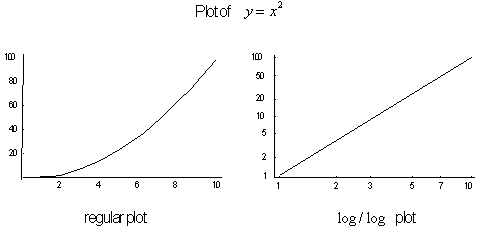
Figure 4.39 Measure
lengths on regular graph vs. logarithmic graph.
As you reduce the length of your measuring "sticks",
the precision of your measurement increases, generally resulting
in a greater apparent length for objects with fractal dimension. For different
objects, you should use an appropriate measuring stick. For example, in
measuring the coastline of Britain you might measure it in units of 1000
km, 500 km, 100 km, 50 km, 20 km. (It is easier, of course, to use maps
with a corresponding scale.) For the circular parameter of a wheel, your
measurement might be in meters 1m, .5m, .1m, .05m, .02m. You might use a measuring tape
as a final measurement, which works well for wheel because there are not
large deviations on the surface.
 |
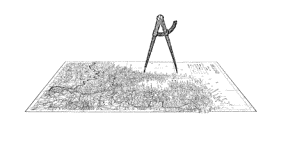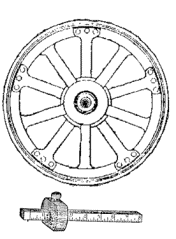
Figure 4.40 Measuring
perimeters using different measuring sticks.
Richardson's
Dimension Equation.
Let's look closer into the Richardson's method for
calculating fractal dimensions using varying measurement lengths. To calculate
a dimension, we first have to establish a logarithmic relationship between
the object's over all 'measured' length and the length of the 'ruler'
used to measure it. We do this by graphing various values of
, where
is the length of the perimeter,
against the corresponding values of
, where
is the scaling factor (the rulers
length), used in measuring the perimeter. The resulting slope of the (
/
) graph will be the related fractal dimension of the measured object.
For a smooth or linear object, smaller rulers will
measure similar lengths as do larger ones, so the slope will be horizontal.
A graph with a horizontal slope corresponds to the dimension
. As the fractal dimension of an object increases, so does the severity
of the slope.
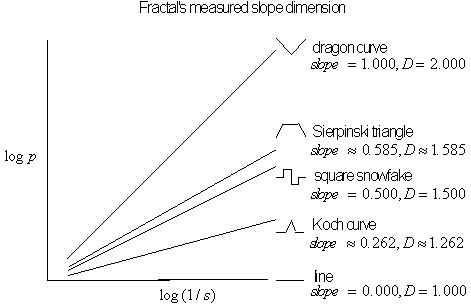
Figure 4.41 Different
slopes of
/
corresponding to different fractal dimensions.
The formula for the Richardson slope method is given
by the relationship
, where
is the calculated slope dimension
of the
graph added to the dimensionally
of a line with value
, and where
is the calculated standard dimension.
Constructing
the Equation in a Familiar Form
Now lets formulate the Richardson equation we have
just seen. Later on we will compare the results with values calculated
from the exact method using the Koch curve.
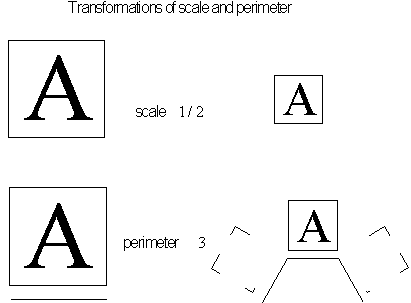
Figure 4.42 Scaling
values and perimeter values
• Select
, the scale value equal to the ratio between the segment's replacement
length and the length of the corresponding seed shape. To plot different
points of the slope, various scales values will be used. Here the scale
measurement values are calculated for higher levels of replacement (a
decrease in ruler length) with the formula
. By using unit levels
, scaling values can be easily calculated that correspond to dimension
.
• Calculate the perimeter length. The length
is given by
.
• Set the two equations equal in terms of the
exponent value
, so
.
• Simplifying we are left with
and
.
•
Now by setting both equations equal to
and then solving, we are left
with a equation
, with the constant equal to
which we set to
.
•
Rewriting the equation we get
or simply the perimeter equation
, where
is the slope dimension giving
in the form
.
Now lets see how to form the relationship
. Remember
and
are interchangeable values.
•
First lets use the perimeter equation
. Taking the logarithm of both sides we are left with
.
•
Next take the equation for the number of line segments
and proceed to put it in the logarithmic
form
.
•
Take the perimeter length given by
, where perimeter length is equal to the number of pieces multiplied by
the scale. Now putting it in its logarithmic form, we derive
.
•
Now by substituting
for
and
for
we are left with
, which simplifies to
.
Now lets construct the Koch curve using the Richardson method and compare the results
with its exact value calculated in the previous section.
Illustrating
the Richardson method using the Koch curve.
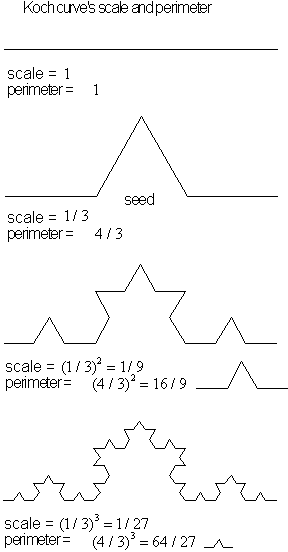
Figure 4.43 Components of calculating the Koch curve.
• Set the scale value of the Koch curve to be
,
.
• The perimeter length of the Koch curve is given
by
,
.
• Setting the two equations in terms of t
results in
.
• Simplifying, results in
and
.
•
Setting both equations equal to
and solving we are left with:
or
.
Then by using an appropriate logarithmic value for
calculating the constant value, in the Koch curve's case
, the results simplify to form a nicely factored equation
[14]
. This leaves the slope for
the Koch curve to be
as seen in Figure 4.44.
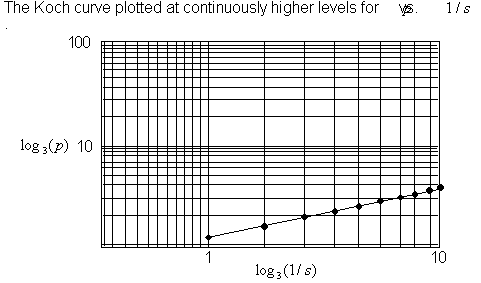
Figure 4.44 The
Koch curve's slope plotted on a
/
graph.
So the calculated value with the Richardson method
for the Koch curve is
. This value is in close agreement with the exact method's calculation
from the previous section. Curiously,
this calculated value is similar to the fractal dimension of Britain's
west coast. In the next section we are going to look at the fractal dimensions
of different states in the United States of America.
The United States
of America and Their Dimensions.
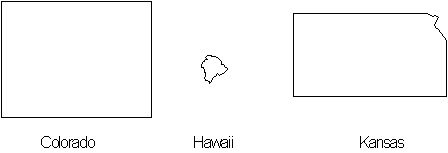
Figure 4.45 Colorado,
Hawaii and Kansas seen in
-dimension plane.
We begin by looking at the different fractal structures
of states in the United States of America. Our first comparison
is between Colorado and Hawaii.
In
-dimensions you can see that Colorado and Hawaii have perimeters that
are quite different. Colorado's boarders are formed by four
straight lines while Hawaii has a rugged coastline. Here we see that a
smaller state can be the one with a longer coastline. In
- dimensions the two states
formations are quite similar with their mountainous terrain, whereas another
state like Kansas, which is basically flat would a have considerably lower
dimension.
Figure 4.46 Colorado,
Hawaii and Kansas seen in
-dimensional space.
Now what happens if we look at California, in
-dimensions it has boarder properties of both Colorado and Hawaii, with
coastal properties on its west side and straight boarders on its east
side. In
-dimensions it shares traits with all three states, by having the mountainous
terrain of Colorado and Hawaii in regions such as the Sierra Nevada Mountains
and the flat plains found in Kansas in its Central Valley. Having more
than one distinctive fractal characteristic puts it in the classification
of a multi-fractal. In a multi-fractal calculation, an object's varying dimensions are measured
and a record is kept of how much of each dimension is found. Multi-fractals
are discussed further in Chapter 6.
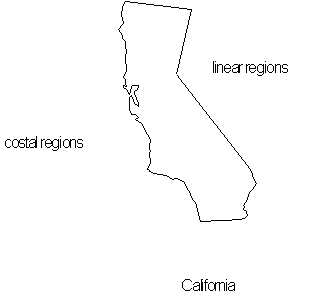
Figure 4.47 California
the multi-fractal
In the following game we are going to look at and then
measure objects for their different fractal dimension.
Measurements, calculating the
dimensions of different objects.
How
long is anything anyway? How long is the coast of Britain, the shore of
Santa Cruz or the length of the Amazon River? As we have seen earlier
the answer depends on what scale you measure them. We typically would
not use the same device to measure a rock as a mountain. For this fractal
experiment you will measure things around you. The measurement sticks
you will need are a tape measure, a foot ruler and a yard stick. If these
things are not available or you want to be unconventional you can use
other things too like a baseball card, sticks of varying lengths, a shoelace,
or almost anything you can find to measure around an object. You can make
up you own units for them, for example: stiff baseball card units, chop
stick units or even 'Fractal Exploration' book units. For units of measurement
are just items with lengths assigned to them. One note: for doing your
calculations, if you use your own units you will have to calculate a length
relationship between the different 'object rulers' you use, such as three
stiff baseball cards are the length of a shoe.
Step 1: Find objects with different dimensions
to measure. For a low dimensional object a flat table is a good choice.
It will serve as a reference source for a standard Euclidean object. For
objects of higher dimension you can use contoured chairs, house plants,
a kid brother or sister, or any other objects with parts sticking out
requiring measurements to be made around those parts. One thing to be
careful of is, since you are measuring a perimeter length you must follow the same path for each measurement.
Step 2: Take each object and measure the
same perimeter for each of your different ruler lengths, recording the
results on your chart as seen in Figure 4.48. This will show you how different
rulers measure different lengths.
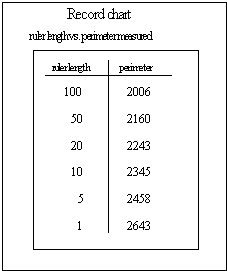
Figure 4.48 Chart
to record the measured lengths of objects from different sized 'rulers'.
Warring: this section is part of a
more advanced exercise and therefore may be skipped. The results vary
widely do in part to your ruler's limited accuracy and scaling range.
The main propose here is to give you an idea on how to physically calculate
fractal dimension using the Richardson method.
Step 3: Take the recorded data you have
recorded of perimeter vs. measured length, convert the data to its logarithmic
values and plot it on a piece of graph paper.
You will find graph paper in Appendix C. Now calculate the slope,
this should roughly correlate to the slope dimension
. Now place
into the equation
to calculate the objects full
perimeter dimension.
We have look at the Richardson Method to calculate
the fractal dimension of an objects perimeter. In the next section we
will use the Box Counting Method of counting area and volume to calculate
an object's fractal dimension.
The Box Counting Method
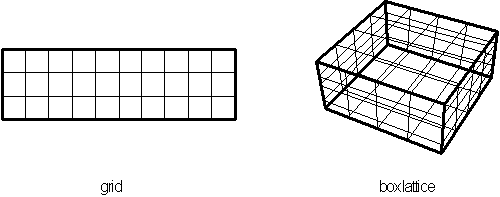
Figure 4.49 Box
counting method using divided segments, grid for a plane space and cube
lattice for a volumetric space.
The Box counting
ratio method ,also known as the Brute force method or Grid Method
is an estimation procedure for calculating the fractal dimension of complicated
objects. It is most effectively used when you cannot calculate an objects
dimension with numerical formulas or accurately determine a slope dimension
of an irregular shapes. For example, it would be difficult to calculate scribbles, dust,
ocean waves, or clouds using other methods. This accounts for its popularity
in spite of its counting resolution's limited accuracy.
Figure 4.50 Some
of the many objects best calculated using the box method.
This method is popular because it is straightforward
and adaptable to many situations. If you can contain an object within
squares or boxes, then you can perform a statistical analysis to determine
its physical dimension. You can
use this method to calculate dimensions for a very small object like Cantor's
dust or for a very large object like a mountain range. You could even
calculate the fractal dimension of the universe--at least what we know
of it.
 |
 |
||
Dimensions Found
in a Plane Space
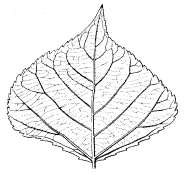
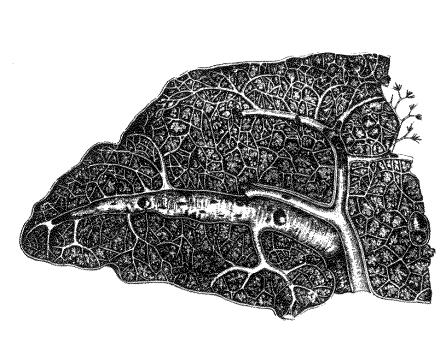
To calculate the fractal dimension of images in a plane,
you begin by covering an
area with grids of different mesh sizes. Then, you
compare the grid sizes and the
number of squares containing at least a part of the
image. The ratio of grid sizes to number of grids containing the object
establishes the dimension.
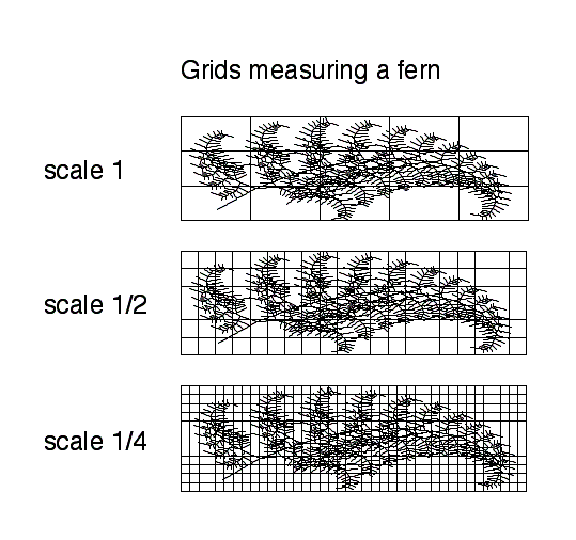
Figure 4.51 Measuring
a fern's dimension with different grid sizes.
Note: Even though this process generally produces accurate
results, there are limitations with this method. For example, if tiles
are used to cover a measured area, the calculated dimension can not exceed
2, because a fractal's dimension
can not exceed the dimension of the units used to measure it.
Dimensions Found
in a Volumetric Space
To calculate dimensions with volumetric space, you
use a similar method as in calculating the dimension of a plane, only
instead of using tiles you use boxes.
These boxes are mapped out to form lattices of varying sizes (
a
- dimensional grid ) called an array see Figure 4.52. Then by counting
the boxes containing at least part of
the object a ratio is established between the box size and its corresponding
count. This ratio at different scales determines the object's dimension.
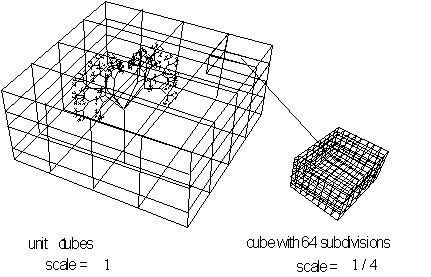
Figure 4.52 Box
counting method for volume a
-dimensional lattice.
Actual Calculations
Now lets examine how the grid method is used to measure
the fractal dimension of an image found in a plane.
•
First, for each grid mesh size, count the number of grids that contain
the image.
•
Now pair all combination of counted
values and place them in the standard equation for the Box Counting Method.
The dimension is calculated by the equation
, where
is the number of squares containing
the image and
is its grid scale. Now average your results to get a good estimate of
the objects fractal dimension. It should be noted that generally finer
grids produce a more accurate measured dimension. This is due in part
to amount of variations that can arise in counting regions dependent on
how a grid is placed see Figure 4.53.
Placing grids in the same position with increased subdivisions
adds in to decrease fluctuations see fern in Figure 4.51.
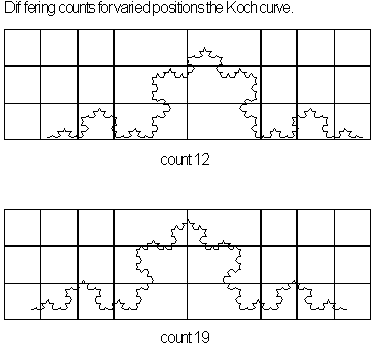
Figure 4.53 Variation
in grid placement.
Alternative method:
• Plot the values of
vs.
on a
graph. Then take the averaged slope as the calculated fractal dimension,
see Figure 4.54.
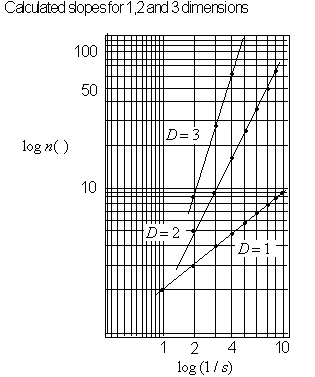
Figure 4.54 Measuring
an objects dimension by comparing values,
vs.
, plotted on a
graph.
You can use the same method for volumetric measurements
of dimension by using cube boxes, as seen in Figure 4.52.
Now lets do the calculations for the Koch curve, and
compare the results to previous methods.
Measuring the
Fractal dimension of the Koch curve Using the Box counting Method.
We begin by counting the number of squares that contain
part of the Koch curve for each grid. Here we use three grids with ratios
1 : 1/2 : 1/4 with counts 18, 41 and 105 as seen in Figure 4.55, Figure
4.56 and Figure 4.57 respectively.
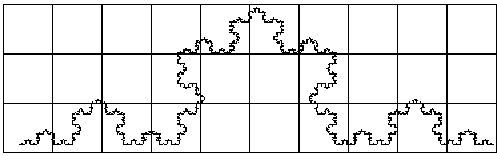
Figure 4.55 The
Koch curve with unit 1 grid size, with 18 containing the curve.
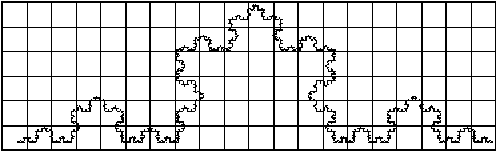
Figure 4.56 The
Koch curve with unit 1/2 grid size, with 41 containing the curve.
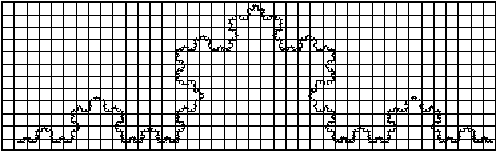
Figure 4.57 The
Koch curve with unit 1/4 grid size, with 105 containing the curve.
I.
.
II.
.
III.
.
Figure 4.58 Calculating dimensions from three different
grids using the Box Counting Method.
Now taking the data from our three grids and placing
them into the Box Counting Equation, we are left with three approximate
calculated dimensions with sizable fluctuations in value see Figure 4.57.
Their average of
is a reasonably close result to
the actual value of
, if you were to do more calculations with different grid sizes you should
expect most values to fall within a certain range. If you were to refine
your measurements further with considerably smaller grids an increase
in accuracy should be reflected in the answer.
In Figure 4.59 we show the dimension of the Koch curve
by counting grid boxes containing the object and graphing the results
on a
plot.
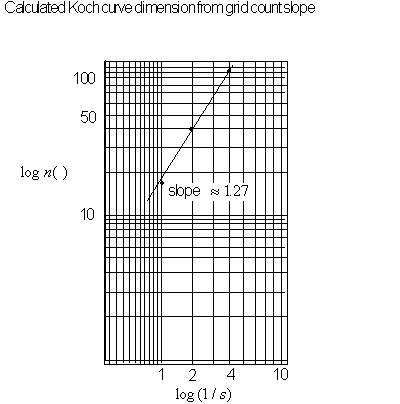
Figure 4.59 Using
the Koch curve data to formulate a slope dimension.
Now we are going to look at different areas of fractal
dimension using a garden vegetable, the Broccoli Romanesco. The Broccoli
Romanesco is an ideal candidate because its fractal structure can be seen
in different ways at several levels of magnification.
The Broccoli
Romanesco, a fractal seen in three different dimensions.
The Broccoli Romanesco exhibits fractal structure in
its perimeter, planar and volumetric dimensions. Lets look at them now.
Figure 4.60 Measuring
the Broccoli Romanesco jagged perimeter.
If we look at the perimeter of the Broccoli Romanesco
we can see an outline that bares a 'rough' resemblance to the Koch curve,
see Figure 4.61. Notice the continuos jaggedness seen at different levels
of magnification even at a close distance. The measurement of the jaggedness
of this irregular boundary is its perimeter dimension. We can measure
its dimension by comparing the number of squares containing its perimeter
at different grid sizes.
Figure 4.61 A
cross sectional view of the Broccoli Romanesco.
In figure 4.61
we see a Broccoli Romanesco as it looks when it is cut in half. This revealing
cross sectional slice gives a view of it planar dimension. By measuring the number of squares that are
filled at different grid sizes a comparison can be made that corresponds
to its planar dimension. Notice its self-similar branching structure that
can be seen to at least 4 levels.
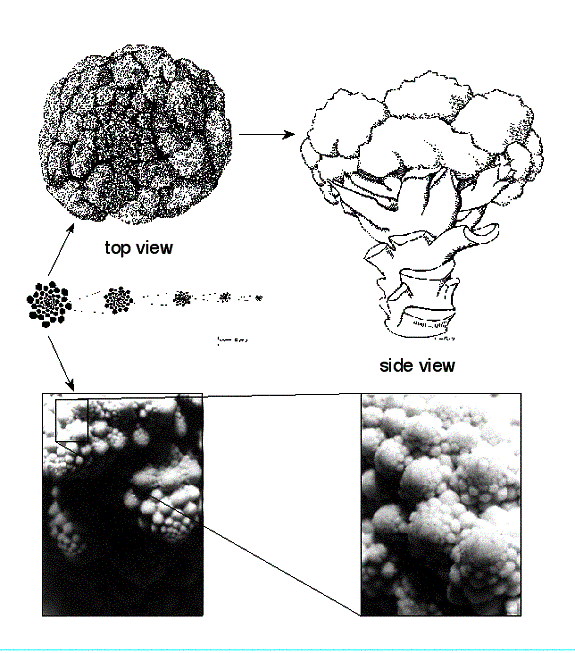
Figure 4.62 Close-up
views of the Broccoli Romanesco at different levels of magnification.
In Figure 4.62 we see a two close-up views of the Broccoli
Romanesco, notice the difficulty in gauging its true size without a scale
reference. In Color Plate 24 we see a Broccoli Romanesco as it looks in
its entirety. This form gives a view of its volumetric dimension. If you
look closely at its top regions you can see the same type of spiral cones
that you see from a distance only smaller. This self similar structure
can be seen to at least 3 levels of magnifications. By creating lattices
at different sizes and counting the number of regions that contain at
least part of the object, calculations can be made that corresponds to
its volumetric dimension. This procedure can be greatly simplified if
the structure's form can be entered and stored as an array of
numbers in a computer. With this alternate way, a computer can
create a mathematical lattice that could partition the object's spatial
values without having to physically divide it.
It is the Box Counting method we use to calculate the
fractal dimension of most things found in nature, see Color Plate
25 to visually compare the dimensions of different clouds. Now lets use
grids to measure planar dimension.
Grid Game for Measuring Dimensions.
In the grid game, you can use the different size grids
found in Appendix C to calculate dimensions of different exact fractals
like we did with the Koch and see how well their dimensions correlate
to their known dimensions. It might come in handy to copy these grids
onto transparencies to use in your calculations if you do not want to
mark your fractals with grid lines. Also
included in Appendix C are various grid maps for Great Britain and the
Monkey tree that can be used to calculate their dimension.
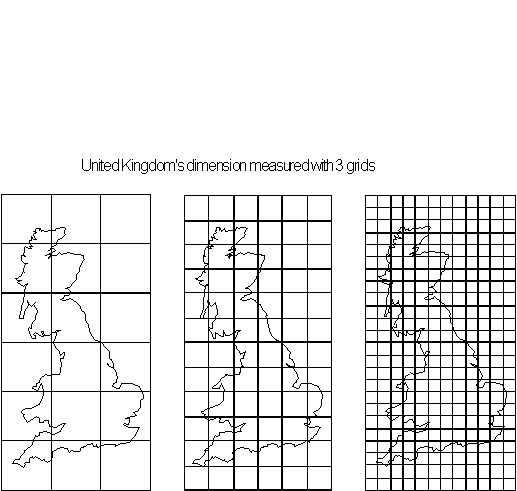
Figure 4.63 Three
different size grids for Great Britain: scale
, scale
and scale
.
Step 1: Find a fractal to measure
whose dimension you know and can be measured by the grid sheet you are
using. This fractal can be one you find in a book ( for example this one
) or one that you create and printout in FractaSketch. In FractaSketch
the dimension value can be read from the menu bar of the program.
Step 2: Take your fractal and divide
it with evenly distributed grid squares with known grid values. A good
technique is to place different grid size transparencies over the object and count the contained squares as seen with
Britain in Figure 4.63. For a basic exercise you might want to start by
carry out calculation using these grids .
Step 3: Count the contained squares
for the different grid sizes, as we did with the Koch curve earlier in
this chapter, and record their values.
Step 4: Place the recorded values
into the formula
and calculate the image's fractal
dimension.
After you feel reasonably comfortable with the accuracy
of your calculated dimensions, you can use this technique to examine other
fractals whose dimensions you do not known exactly--such as a fern, counties
on a map or even a newspaper. Remember due to the limited accuracy of
our measurements, dimensional values within 10% of the correct value are
consider quite reasonable.
Grid Game for Measuring Dimensions on the Computer.
In the same way you can calculate dimension by using
grids on paper, you can also calculate the dimension of images using a
Macintosh paint or graphics program.
Step 1: Paste an images from FractaSketch, MandelMovie or even an image
of a scanned photograph onto the pallet on your paint program. Save the
image now, so you can recall it for every new grid placed if you need
to, you might want to make a backup copy of your picture in case accidentally
alter it or save it with a grid on it.
Step 2: If your paint or graphics program does not include an option for
creating grids with varying mesh sizes, make the grids first in the program
and paste them in from the "�" menu in your "Scrapbook".
Make 5 grids in sizes of 25, 20, 15, 10 and 5 pixels square. You
can make alternate size grids if you want. It is important when pasting
the grids over the object that the white regions not be included. This
is done by setting the white regions to be transparent in your paint or
graphics program. This will allow
you to see the object after the grids have been placed. Instructions on
how to do this should be found in your paint or graphics program.
Step 3: Place a grid divided into squares of equal size (say 25 pixel square)
and count the number of squares that contain part of the curve. Repeat
the experiment by counting how many squares contain the object when the
grids are 20 pixels square, then 15 square , then 10 square, then 5 square.
If your program does not generate grids you will have use five duplicate
picture files or reopen the picture file each time without saving the
changes of the added grid.
Step 4: Count and record the number
of squares containing the object for the different grid sizes.
Step 5: Place the recorded values
into the formula
and calculate the image's fractal
dimension.
Step 6: If you know the fractals dimension in FractaSketch, compare the
results and see how close they correlate.
The fractal dimensions calculated here are averages
of the whole structure and can not discern between the dimensions of its
different regions. This type of work deals with multi-fractals.
[15]
which we will see with greater
detail in Chapter 6.
We have looked at 3 major ways of calculating fractal
dimension.
• Calculations of exactly self-similar
dimension, using mathematical formulas.
• Richardson's dimensional
measurements of divided segments. Here fractal dimensions correspond to
the slope correlating to the length of the "ruler" used and
its overall measurement.
• Box-counting dimension, calculating the containment of an object at different measurements.
In the next chapter we will look at ways to generate
fractals with equations. This procedure is responsible for producing many
of the colorful fractals that almost defy description. In Chapter 6 we will look at fractals with the similar shapes and
dimensions to the ones we have calculated in this chapter. These fractals
are generated by taking points and mapping them to other regions, we call
this technique Iterated Function Systems.
[1] From Newton's work, Philosophie Naturalis Principia Mathematica, Praefat. [2] Mathematica 3D graph of Plot3D[Sin[x y],{x,0,Pi}, {y,0,6},PlotPoints -> 30]. [3] From the revised 2nd edition of Flatland published 1884. [4] Initially fractal geometry was classified as a field in topology. However, as it evolved it became heavily in twinned into other areas of mathematics, most notable dynamical systems. Fractal geometry is now used in analyzing many of the structures found in chaos theory.
[5]
Often
[6] In The Fractal Geometry of Nature, 1982 page 46, Benoit Mandelbrot refers to The Gosper Island as The Koch Island or Lake. Originally the curve was named " The Gosper's flowsnake" for its discoverer William Gosper in an article " Monsters" by Martin Gardner published in December 1976 Scientific American article pages 124-133. [7] Also called " snowflake halls". [8] Written in 1922 as an annotation to his work in turbulence. According to Benoit Mandelbrot's book The Fractal Geometry of Nature, 1982 page 402 this passage is often quoted anonymously due in part to " ... their kinship to some classics." See a poem on fleas, from which this poem was parodied also on page 402. [9] It was Richardson's work that prompted Mandelbrot and others to ask the now famous question 'How Long is the Coast of Britain ?'. Benoit Mandelbrot wrote a well known paper 'How Long is the Coast of Britain ?' in which he proposes many original ways of discussing fractal geometry (1975). [10] These measurements were made by scanning in a country's map ( this case Britain ) and then using the draw program's built in segment length measuring tool as the method for making measurements. [11] It is believed that Richardson noticed many discrepancy in territorial measurements when he was trying to build models on why nations have conflicts that result in war. Richardson spent a great deal of his life's work on peace and conflict studies mainly on why nations go to war. This is quite understandable considering he lived his life in England experiencing both World War I & II. [12] Page 27 Mandelbort's The Fractal Geometry of Nature. The problem of contiguity: an appendix of statistics of deadly quarrels, General Systems Yearbook 6 (1961) pages 139-187 [13] You will find the term epsilon used.
[14]
We can write
[15] Benoit Mandelbrot, An introduction to multi-fractal distribution functions, found in: Fluctuations and Pattern Formation, H.E. Stanley and N. Ostrowsky, Kluwer Academic, Dordrecht, 1988. J. Feder, Fractals, Plenum Press, New York 1988. K. Falconer, Fractal Geometry, Mathematical Foundations and Applications, Wiley, New York, 1990. |
is referred to as the natural log and is derived from the limit
.
.
